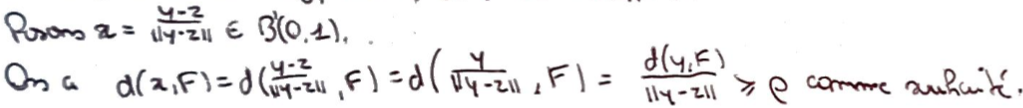On prend \(y\in E\setminus F\) \(\to\) la distance de \(y\) à \(F\) est bien définie puisque \(F\) est fermé.

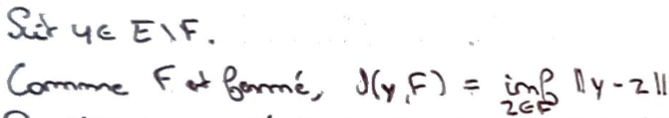
Par définition de l'\(\inf\), on a l'existence d'un \(z\) qui vérifie la relation.

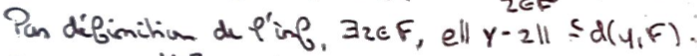
Si on pose \(x\) en normalisant la différence entre \(y\) et \(z\), alors on a bien ce qui est demandé.

Dans ce cas, on peut montrer que \(F\) est complet, et donc fermé.

L'\(\inf\) de la distance est bien atteint car il agit sur un fermé borné (compact).

On conclut en posant \(x\) en normalisant \(x-y\).